合成抵抗とは?
電気回路を学ぶうえで、欠かせないキーワードのひとつが「合成抵抗」です。
これは、複数の抵抗を一つにまとめて考える方法のことです。
合成抵抗を知っておけば、回路の電流や電圧の計算が楽になります。
抵抗とは何か?
まず「抵抗」について確認しましょう。
抵抗とは、電流の流れにくさを表すもの。
単位はオーム(Ω)です。
合成抵抗の求め方は、抵抗の接続方法によって異なります。
大きく分けて以下の3つがあります。
1.抵抗の直列接続
接続方法
抵抗を一列で接続する方法を直列接続(series connection)という。
接続図
回路図では、抵抗が一直線に並んで描かれます。

特徴
・電流は等しい。
・電圧は分圧する。
計算式
直列接続では、合成抵抗R₀は単純に抵抗値を足し算するだけです。
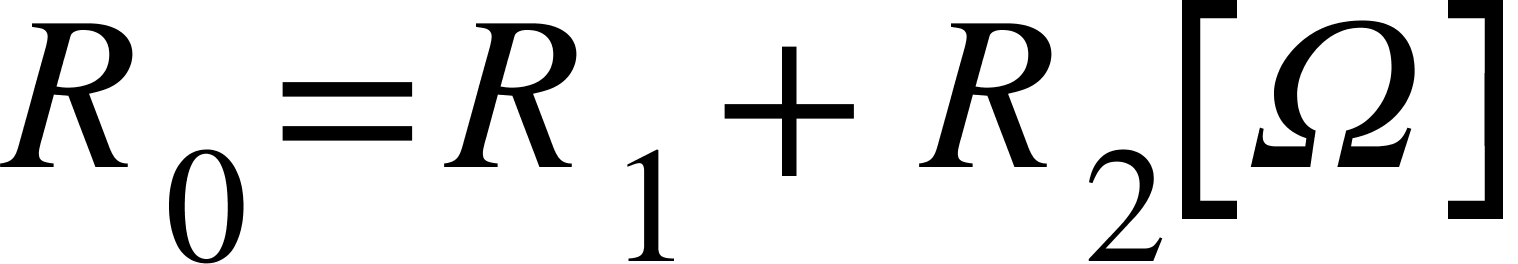
例題
R₁=10ΩとR₂=20Ωの抵抗を直列に接続すると…

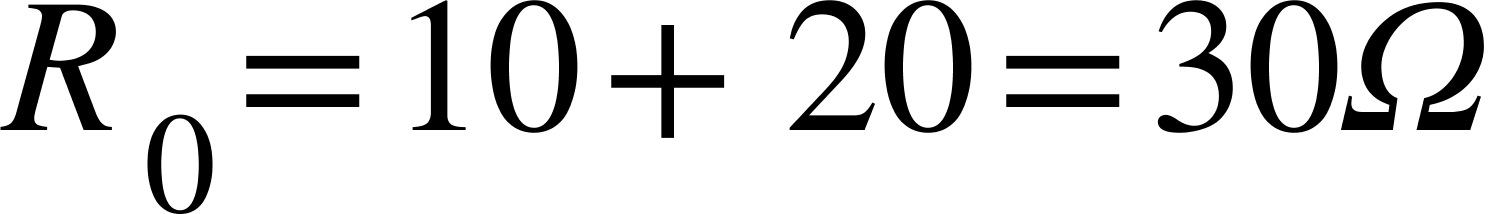
2.抵抗の並列接続
接続方法
抵抗を並べ、それぞれの両端をまとめて接続する方法を並列接続(parallel connection)という。
接続図
回路図では、抵抗が横並びに描かれ、両端が共通の配線に繋がっています。
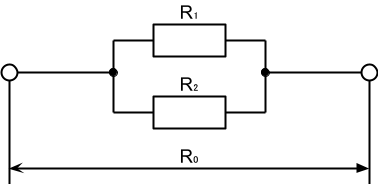
特徴
・電圧は等しい
・電流は分流する
※直列接続の特徴とは反対なので、混乱しないように覚えましょう!
計算式
並列接続では、逆数の和を使うのがポイントです。
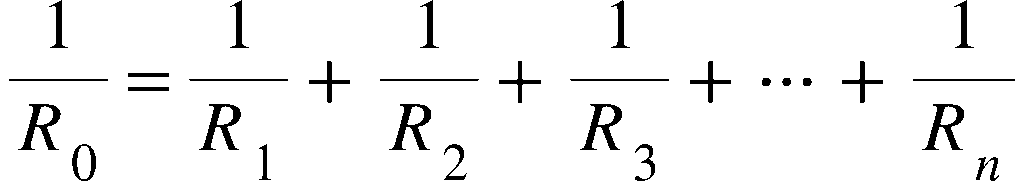
2つの抵抗だけの並列接続のときは、和分の積も使えます。
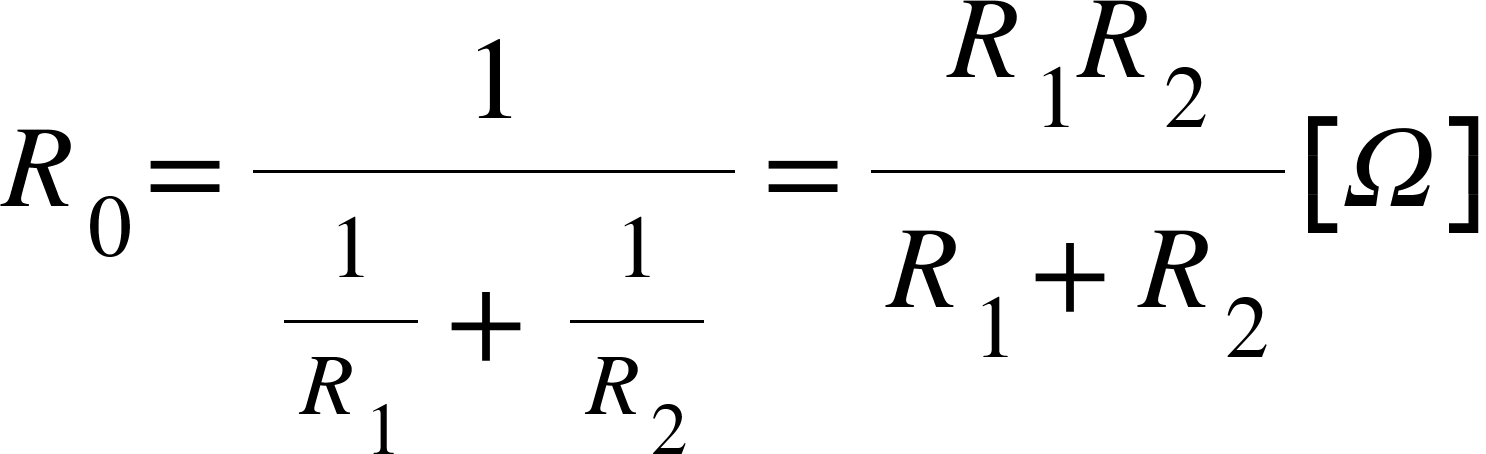
例題1(並列2つ接続の時)
R₁=80ΩとR₂=20Ωの抵抗を並列に接続すると…
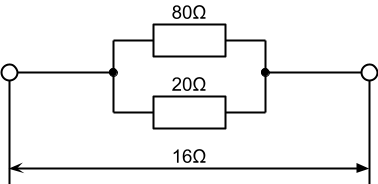
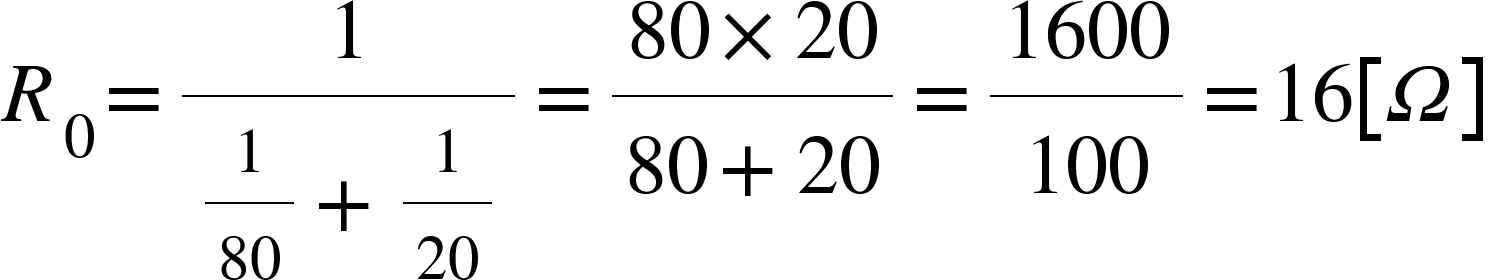
例題2(並列3つ接続の時)
R₁=80ΩとR₂=20ΩとR₃=10Ωの抵抗を並列に接続すると…

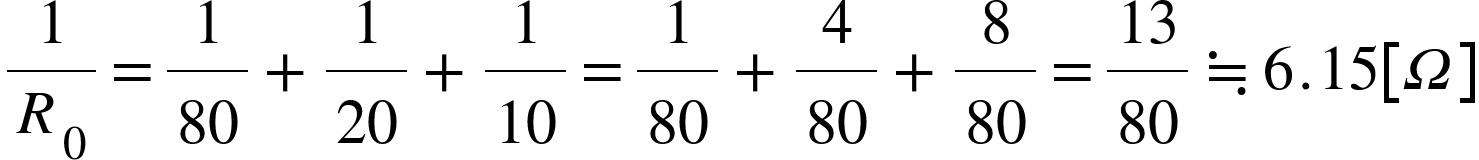
3.抵抗の直並列接続
接続方法
直列接続と並列接続を組み合わせた接続方法を直並列接続という。
より複雑な回路では、この直並列接続がよく登場します。
接続図
直列と並列が組み合わさった回路図になります。

特徴
直列部分は足し算、並列部分は逆数の和を使って計算するのがポイントです。
例題
R₁=30ΩとR₂=20ΩとR₃=10Ωの抵抗を直並列に接続すると…
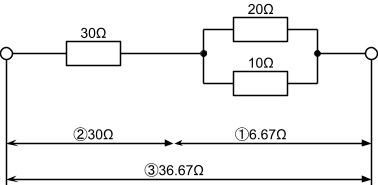
計算方法
まずは①並列に接続されている部分を見つけて計算します。
抵抗が2つ並列接続されているので、和分の積が使えますね!
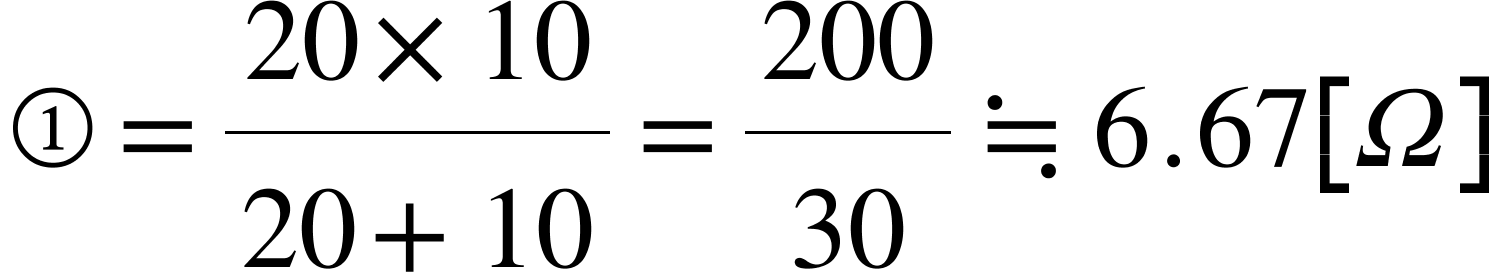
次に②の値を求め、、
って直列なので、そのままですね!
![]()
最後に③の値を求めるのですが、
まず、接続図を簡単にまとめましょう。

こうしてまとめた図のことを等価回路と言います。
等価回路にしてみれば、もうおわかりいただけただろうか、、
そう、直列接続図になってますね!
ということは、後は足すだけです。
![]()
このように、段階的に計算していくのが直並列回路のポイントになります。
まとめ
合成抵抗は、複数の抵抗を一つの抵抗委置き換えて考える便器な方法です。
直列接続では足し算、並列接続では逆数の和を使うと覚えておきましょう。
直並列接続では、先に並列部分の合成抵抗を計算してから直列部分を足し算するのがコツです。
電気回路の計算になれるために、実際にいろんな例題を解いてみるのがおすすめです。
応用問題1
R₁=8Ω、R₂=16Ω、R₃=48Ω、R₄=60Ω、R₅=30Ωのとき、合成抵抗(R₀)の値を求めよ。
下記にて解説をしますが、一度考えて解いてみてください。

まずは、並列部分を探しましょう。
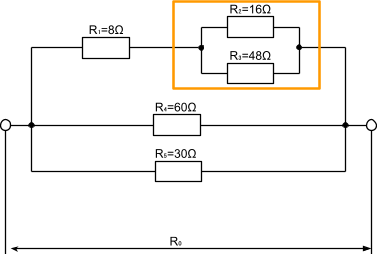
橙枠ですね。
2つ並列接続なので、和分の積が使えます。
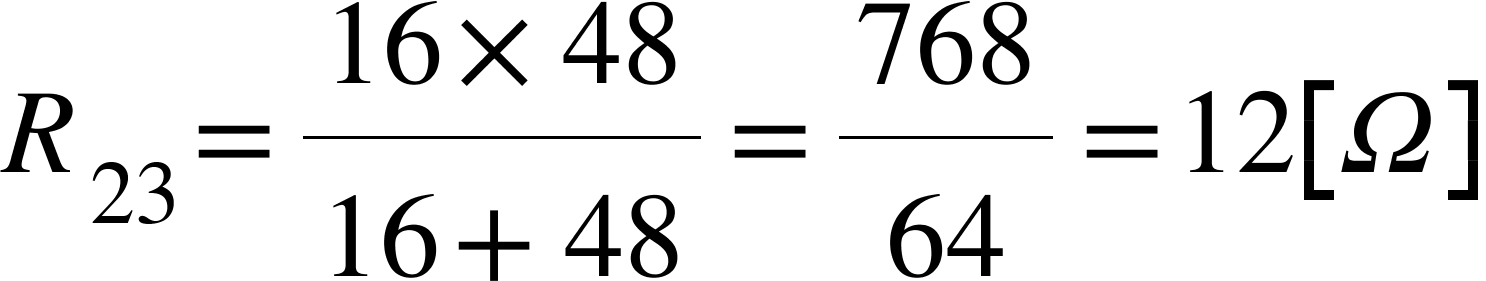
並列部分の値が出ましたね。
それでは、一度回路図を整理してみましょう。

パッと見て並列接続に見え、並列で計算したいですが、
まだ上部に2つ抵抗があります。
なので、先に上部の直列部分を計算しましょう。

直列接続なので、足し算でいけますね。
これで、やっと並列計算できますね。
その前に、一旦回路図を整理しましょう。
だいぶスッキリしましたね。
後は3つ並列接続の計算するだけです。

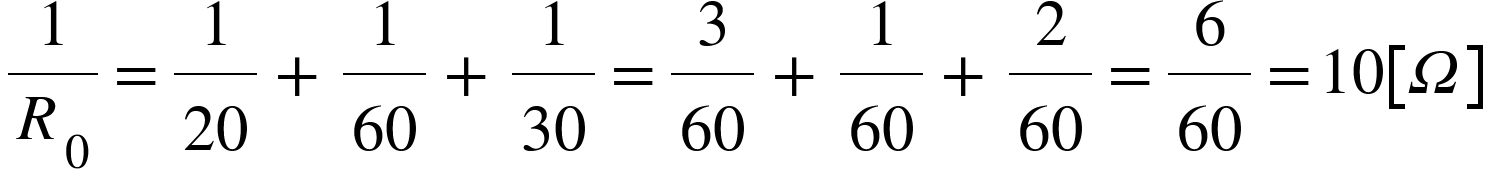
答えは10Ωでした。
合っていましたか??
回路図を頻繁に整理していますが、
慣れてきたら、そのまま整理せずに計算できるかと思います。
まだ慣れないよって方は、□で囲むのも一つの手ですね。
応用問題2
a-b間の合成抵抗が3Ωの場合、抵抗Rの値を求めよ。
次は合成抵抗から抵抗値を逆算してみましょう。
これができたら、合成抵抗は完璧ですね!

まずは回路図を部分分けして考えましょう。
(a)橙、(b)青、(c)赤で部分分けしました。
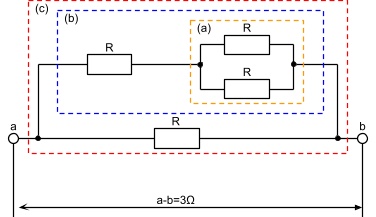
(a)並列部分から計算してみましょう。
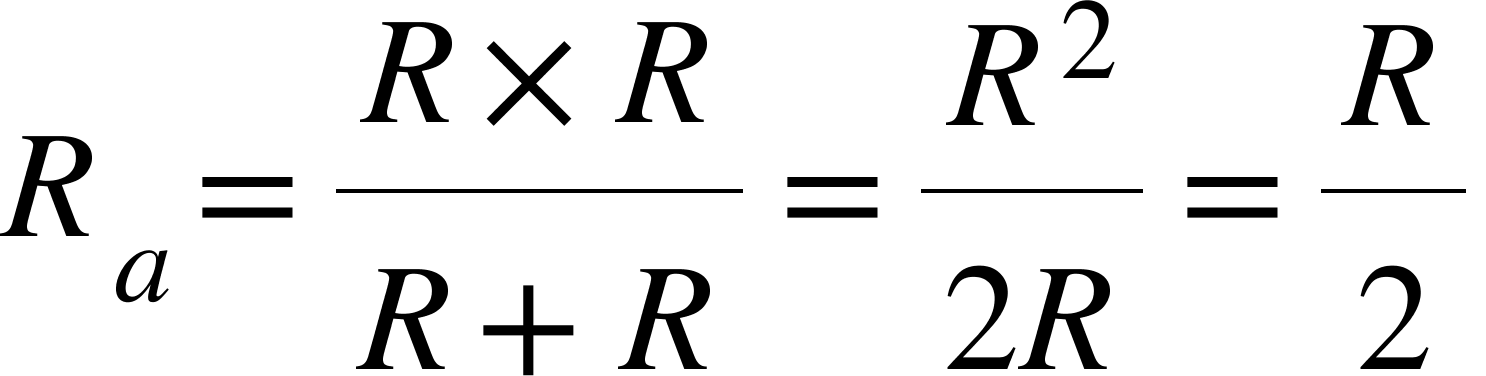
(b)次は直列部分の計算になります。
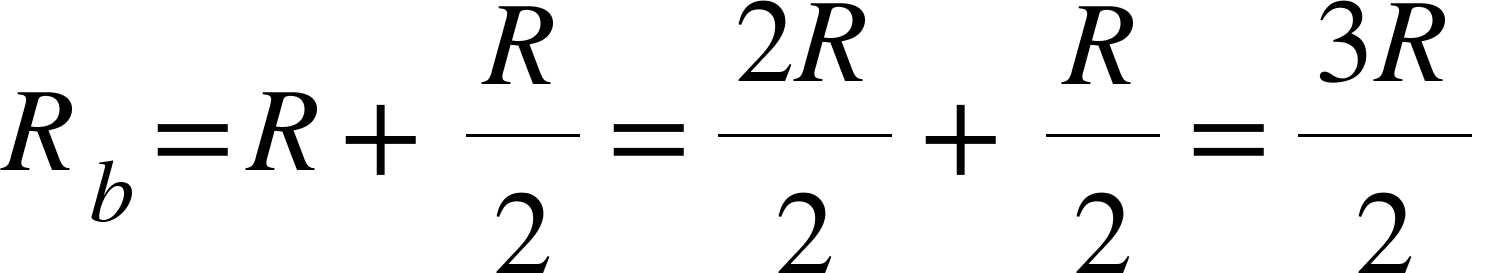
(c)最後は並列部分の計算になります。
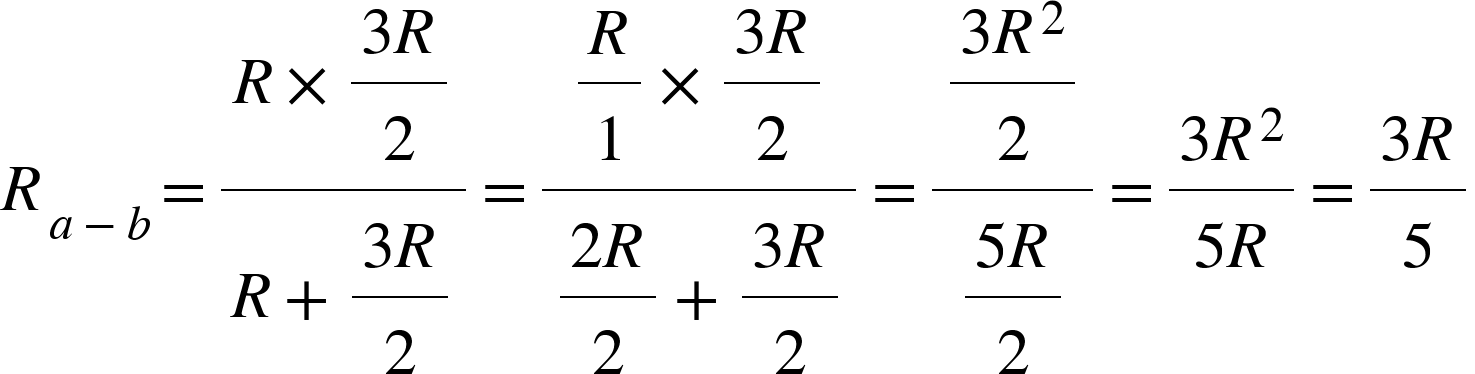
a-b間の計算式が出ましたね。
それでは合成抵抗=3からRを求めましょう。
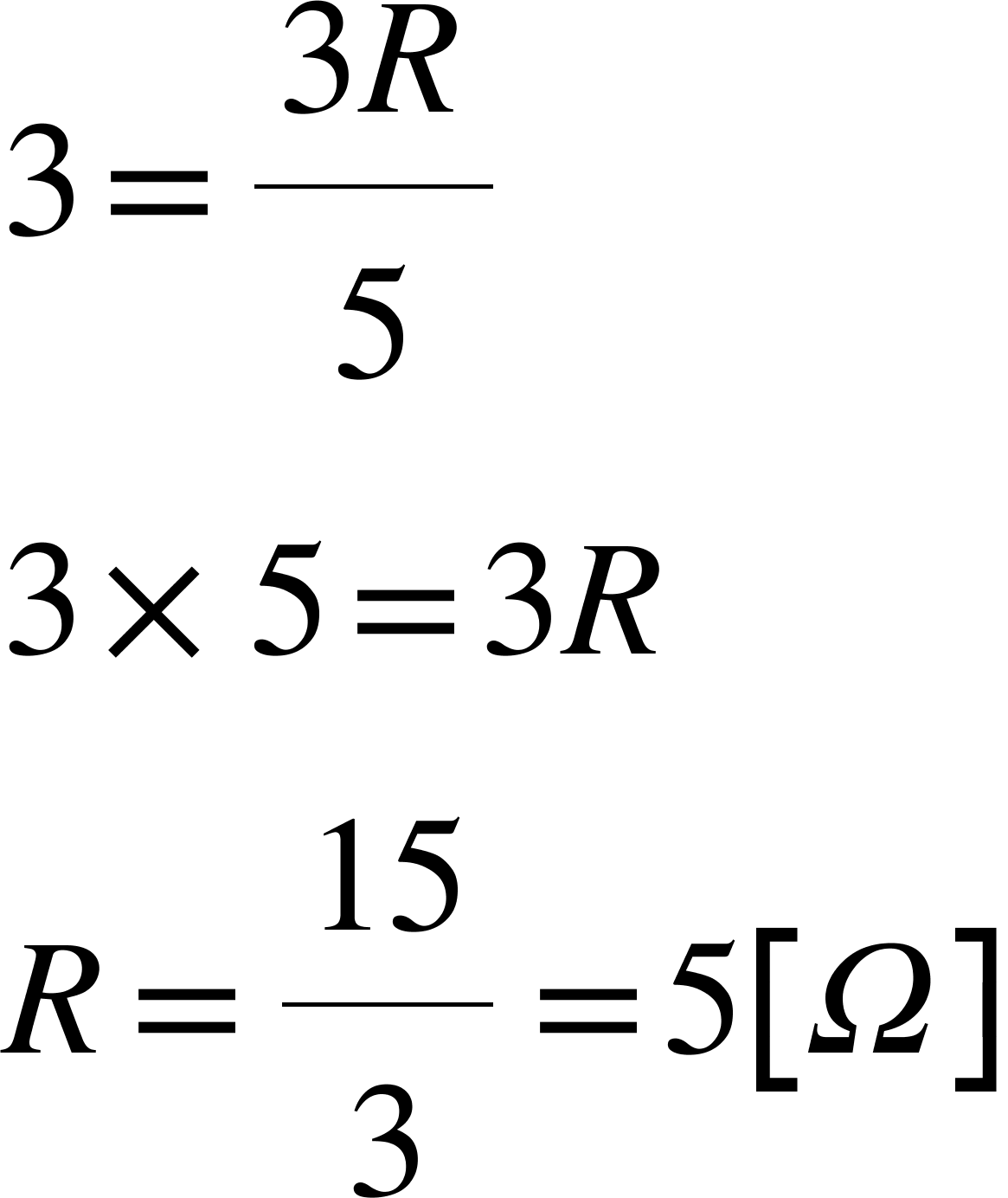
答えは5Ωでした。
正解しましたか?
最後に
今回は合成抵抗について解説しました。
分圧と分流はまた今度、別記事にて解説します。
最後までお読みいただき、ありがとうございました。



